Chyba właśnie funkcjonalność jest tu sprawą kluczową. Nie odkryję raczej Ameryki pisząc, że kostka obiekt służący do losowania. Jak już ustaliliśmy, ilość ścianek może być bardzo różna, ale raczej dobrze by było żeby wszystkie miały identyczne lub liniowo symetryczne kształty. No i żeby przynajmniej prawdopodobieństwo wypadnięcia każdego możliwego wyniku było identyczne. Oczywiście mówię tu o kostkach uczciwych, bo są i nieuczciwe. Można bez większych problemów kupić kości obciążone, na których prawdopodobieństwo wypadnięcia pożądanego wyniku jest celowo poprawione przez przesunięcie środka ciężkości.
W tym miejscu warto wspomnieć, że istnieją także kostkowe dziwaki w formie, o której była mowa ostatnim razem (graniastosłup o podstawach w kształcie wielokątów) z tą różnicą, że nie turla się nimi, a zwyczajnie rzuca, a proporcje krawędzi są tak dobrane, że prawdopodobieństwo, że kostka zatrzyma się na jednej z wielokątnych podstaw jest takie samo, jak to, że zatrzyma się na którejś z prostokątnych ścian bocznych. Teoretycznie niby ok, ale mnie osobiście taki koncept nie pasuje, bo widzę możliwość oszustwa przy rzucaniu - myślę, że nadanie kostce rotacji w płaszczyźnie równoległej do podstaw może zmniejszyć prawdopodobieństwo lądowania kostki na podstawach, a tym samym wpłynąć na wynik. Wiem, że podobny zarzut można postawić choćby wobec k6, ale moja wątpliwość i tak pozostaje.
Zdarzają się też kości różnościenne, które są jednak tak skonstruowane, że na niektórych ściankach się nie zatrzymują. Przykładem może być tutaj rzadko spotykana forma k4. Jak wiadomo, żeby wynik standardowej k4 odczytuje się nie z płaszczyzny u góry (bo takiej płaszczyzny nie ma), tylko z opisów umieszczonych na ściankach, które po rzucie znalazły się bezpośrednio przy powierzchni, na której kostka wylądowała. Ktoś wymyślił, że wcale nie musi tak być i wymyślił, żeby odpowiednio ściąć wierzchołki, a potem na tych miejscach umieścić wyniki. Taka bryła nazywa się czworościanem ściętym i, jeśli idzie o ścisłość, jest bardziej ośmio- niż czterościanem. Jej ściany to cztery trójkąty równoboczne, powstałe w miejscu wierzchołków i cztery sześciokąty foremne, w miejscu dawnych, trójkątnych ścian.
Licencja: CC BY-SA 3.0
Można dodać jeszcze, że taka bryła należy do wielościanów półforemnych albo archimedesowych. Wikipedia pisze o tym następująco (link w bibliografii pod artykułem):
"Wielościan półforemny (albo archimedesowy – od imienia Archimedesa z Syrakuz) – wielościan, którego ściany są wielokątami foremnymi, w każdym wierzchołku zbiega się jednakowa liczba ścian, jednak poszczególne ściany różnią się od siebie oraz istnieje izometria przekształcająca każdy wierzchołek na każdy inny (...)"
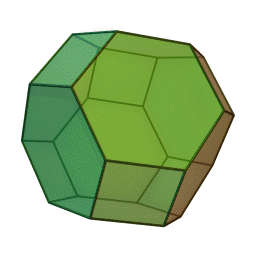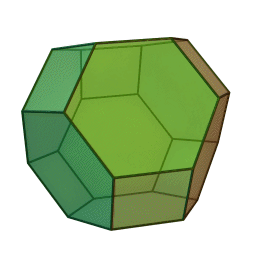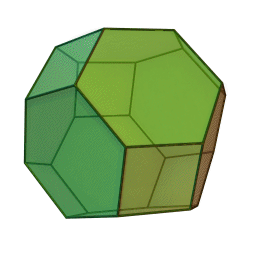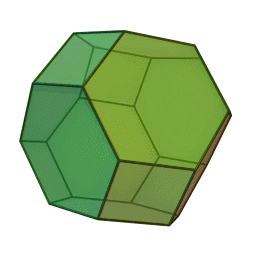
Podobne wariacje można też zrobić z k8, przy czym w związku z faktem, że k8 ma wszystkie ścianki równoległe parami, jest to bardziej udziwnienie, niż funkcjonalność. No, może tyle, że jest mniej "rogata" i lepiej się turla. Taka przerobiona kaósemka ma osiem ścian w kształcie sześciokątów (dawne trójkątne ściany o poobcinanych rogach) i sześć ścian w kształcie kwadratów. Zapewne na tych dwóch przykładach możliwości się nie kończą, chociaż nie przychodzi mi do głowy inna kostka zbudowana na tej zasadzie. No, może odrobinę pokrewna jest idea kształtu części kaszóstek, które przecież nie są sześcianami, a raczej kulkami ze ściętymi na kształt sześcianu wypukłościami...
Licencja: CC BY-SA 3.0
Na tym koniec na dziś. W bibliografii oprócz artykułów na wikipedii pozwoliłem sobie na podlinkowanie dwóch stron zagramanicznych producentów, którzy robią takie dziwne kostki. Oczywiście można wyguglać więcej podobnych stron, ale akurat na te strony zerkałem podczas pisania.
O interpretowaniu wyników jednak będzie innym razem, bo, nawet przy tak pobieżnym traktowaniu tematu, można jeszcze sporo napisać o formach i kształtach kostek.
Pierwsza część artykułu Kości, kostki, kosteczki... : http://kaszostka.blogspot.com/2016/03/kosci-kostki-kosteczki.html
Bibliografia:
https://pl.wikipedia.org/wiki/Ko%C5%9B%C4%87_do_gry
https://pl.wikipedia.org/wiki/Wielo%C5%9Bcian_p%C3%B3%C5%82foremny
https://pl.wikipedia.org/wiki/Czworo%C5%9Bcian_%C5%9Bci%C4%99ty
https://pl.wikipedia.org/wiki/O%C5%9Bmio%C5%9Bcian_%C5%9Bci%C4%99ty
http://thedicelab.com/UniqueDesigns.html
http://www.koplowgames.com/



Ciekawa ta seria :)
OdpowiedzUsuńKoyoth, czekamy na kolejną część! :-)
OdpowiedzUsuń